Batch 3 - Class 207 -King Kong and City Skyline
Pre-Class Exercise
- Think about three point perspective, and how you would see a tall building for example. What is the third dimension that could be subject to perspective?
- Three point projection - a box where eye is not aligned to the base of box
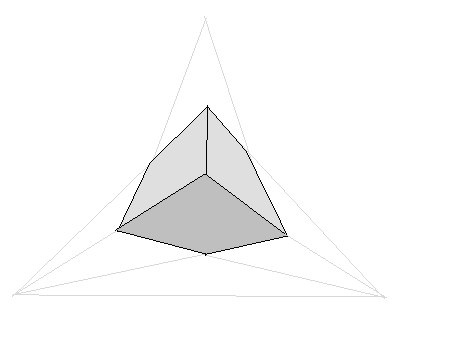
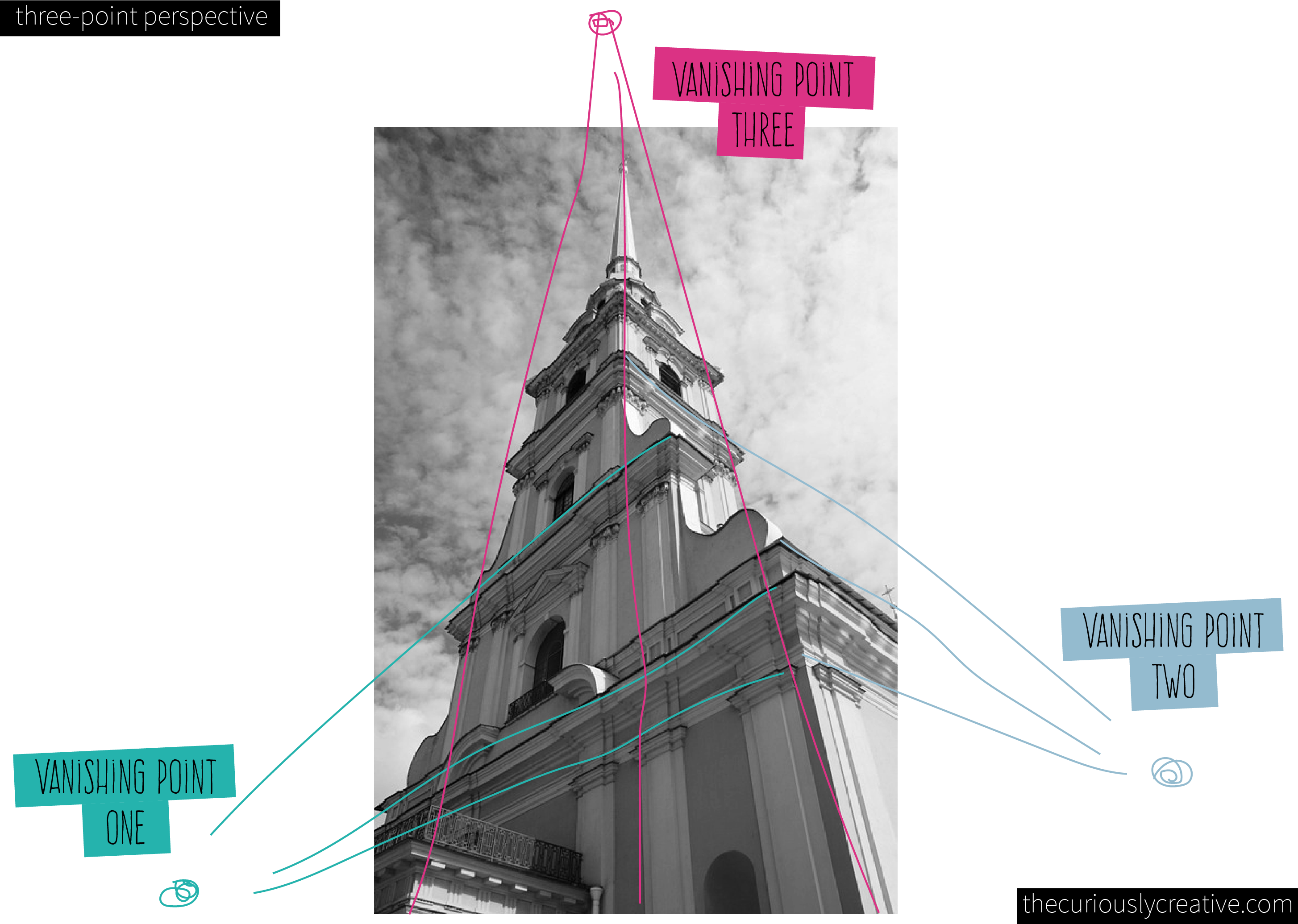
- Think of a tall building or tower or church, and draw a three point perspective
Attendance Rohan, Kabir, Kushagra, Vansh, Aashvi, Muskaan, Advay, Rhea
Class puzzles (Repeat from Class 111)
King Kong and City Skyline (aka Bulgarian Solitaire Patterns)
King is out in the city. King Kong removes the top floor from every skyscraper, and makes a new skyscraper out of these floors. He then organizes all the skyscrapers tallest to shortest. He then keeps repeating the process. For example, with 7 skyscrapers, following sequence denotes the first few steps.
.png)
Complete the above. See what happens. You will see that the following cycle is created.
.png)
If we started with 25 blocks, will we get a cycle? How long?
Lets try and make these for all numbers up to 11. We will notice the length of cycles we create. Tabulate them.
- Instructor Notes: For 8, kids may come up with two solutions, a 2-cycle and a 4-cycle. For now, ignore it as an anomaly and tabulate the larger 4-cycle.
For some numbers, there is a stable pattern that emerges. Which are these numbers? Can you find a pattern. Can you describe why these are stable?
- Answer: Triangular numbers (1,3,6,10...) have stable patterns. One can understand these by looking at a city like 4,3,2,1 and seeing that it keeps recurring
Cycles seem to gradually increase. Can you find a pattern to these?
Look at all numbers "1 less" than triangular numbers - can you find a pattern of increasing cycle size? Can you see why it happens?
- Answer: "1 less" number patterns are nothing but the triangular pattern, with 1 story taken out from successive towers. Think of this as the bottom story being taken out rather than the top, because King Kong will always find a top story to pick
.png)
- The way to think about the shifting of the "taken out" story is that when King Kong picks the diagonals (top story of each building), that new building is inserted to the left, and hence every other building shifts one right, and with it the "taken out" story shifts one right.
Look at all numbers "1 more" than triangular numbers - can you find a pattern of increasing cycle size? Can you see why it happens?
- Answer: Similar to above, this involves adding in one more story successively to each tower. One more tower can get added at the end, which is what bumps up the cycle size.
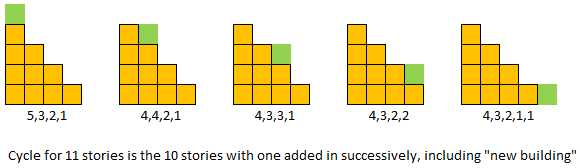
Interestingly, if you try to draw with 8 stories, this is same as taking the 6 story "stable solution" and trying to add 2 more stories across the tower (3 existing and 1 potentially new) - 4C2 is 6, so there are 6 ways of doing it. These form a 4-cycle and 2-cycle as shown below. Note that adding two stories to first tower itself leads to a configuration which is not in the cycle, since there are only 4 buildings and hence a 5 story building can not be formed from a cycle configuration.
.png)
Similarly, for 12 stories (10+2), we need to add 2 stories to 10 pattern across 5 buildings. This can be done in 5C2, i.e. 10 ways. This gives us 2 cycles of 5 configurations each.
Can you predict what cycle length will be formed for 25 skyscrapers?
- Answer: 7-cycle - there are multiple of these. One should be able to come up with these by starting with 21 and adding 4 stories to the 7 positions possible. This can be done in 7C4 ways, i.e. 35 ways. Each cycle being 7 long would imply 5 potential cycles, but I have not validated that.
.png)
Homework
- How can you divide a long paper strip into 5 equal parts?
- Answer: start with an approximation from one end. Then fold the far end into four parts. The new 1/5th estimation is better than the old one. Repeat few times to get a good approximation of 1/5
References: